本篇主要介绍一个鼠标追踪的小程序。程序的GUI（graphic user interface ）部分是用python的tkinter来实现，追踪算法是用卡尔曼滤波器来实现。
在正文之前，我首先致谢(ackownledge)我所采用的参考资料。程序部分主要参考了Richard Teammco的JavaScript代码，我对其中极小的错误进行了修改, 删减了我认为不重要的功能。因为本人当时不会JavaScript，所以我改成了python的代码。GUI动画的引擎借鉴（基本照搬）了Irmen de Jong的程序。
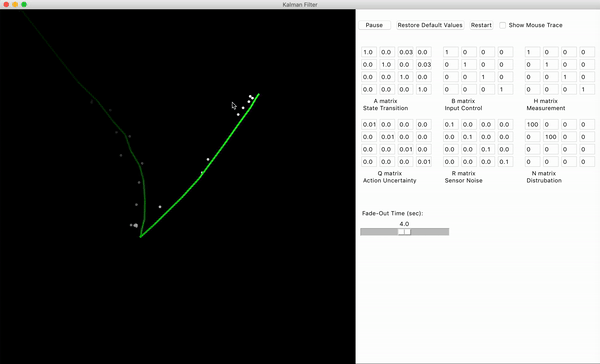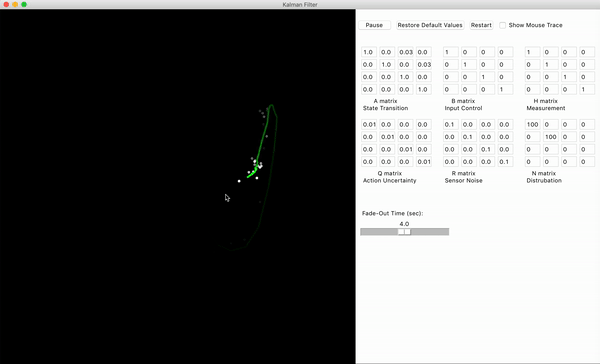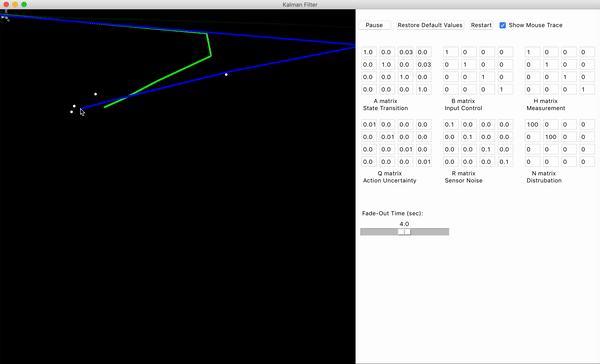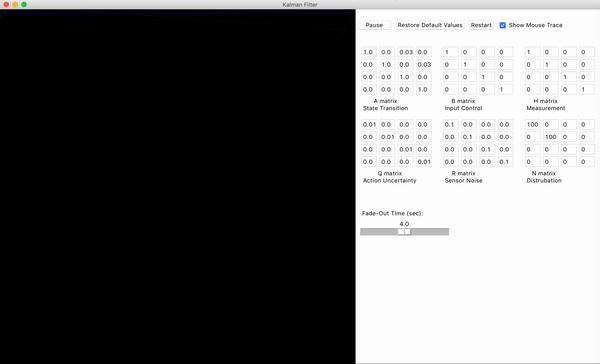
程序的效果如图所示，代码可以自取。
卡尔曼滤波器简介
模型
有关卡尔曼滤波器的介绍已经很多了，其中底层的模型类似于隐马可夫模型，中文维基百科的介绍就很好。在这里我就不班门弄斧了，只是简略地描述一下。
卡尔曼滤波器模型假设有一个真实的状态$\mathbf{x}_k$，这个真实的状态是从前一个状态$\mathbf{x}_{k-1}$演化过来的，同时也存在一个控制单元$\mathbf{u}_k$对状态$\mathbf{x}_k$进行不断地调整。前面这段话对于初学卡尔曼滤波器的同学可能很难理解，这里举个例子，比如说我要追踪一枚弹道导弹，这枚弹道导弹的状态$\mathbf{x}_k$包括两部分组成，位置和速度。受到惯性的作用，这枚导弹的位置和速度肯定是前一个状态$\mathbf{x}_{k-1}$演化到的。导弹在飞行的过程中又受到了地球引力和导弹控制单元的影响，我们可以把这些影响（也就是加速度）囊括在矢量$\mathbf{u}_k$中。假设整个演化的过程是线性的，那么$\mathbf{x}_k$满足下式
\[\mathbf{x}_k = \mathbf{A}_k\mathbf{x}_{k-1} + \mathbf{B}_k\mathbf{u}_k + \mathbf{w}_k, \tag{1}\]其中$\mathbf{A}_k$是作用在状态$\mathbf{x}_k$的转化矩阵，$\mathbf{B}_k$是作用在控制单元$\mathbf{u}_k$的控制矩阵，$\mathbf{w}_k$是过程的噪声，可以认为噪声符合多维正态分布$\mathbf{w}_k \sim N(0, \mathbf{Q}_k)$。基本的卡尔曼滤波器模型是线性的，当然真实的物理很少是线性的，比如说刚才举例的弹道导弹的例子，由于不可忽略的空气阻力的存在，并且空气阻力和速度有复杂的非线性的关系，模型一定是非线性的，这里我就不做展开了。在每一个时刻$k$，我们都会对状态$\mathbf{x}_k$进行一个测量，
\[\mathbf{z}_k = \mathbf{H}_k \mathbf{x}_k + \mathbf{v}_k, \tag{2}\]其中$\mathbf{z}_k$是测量状态，$\mathbf{H}_k$是把真实空间映射到观测空间的转换矩阵，$\mathbf{v}_k$是观测过程中的噪声，同样也认为满足多维的正态分布$\mathbf{v}_k \sim N(0, \mathbf{R}_k)$。
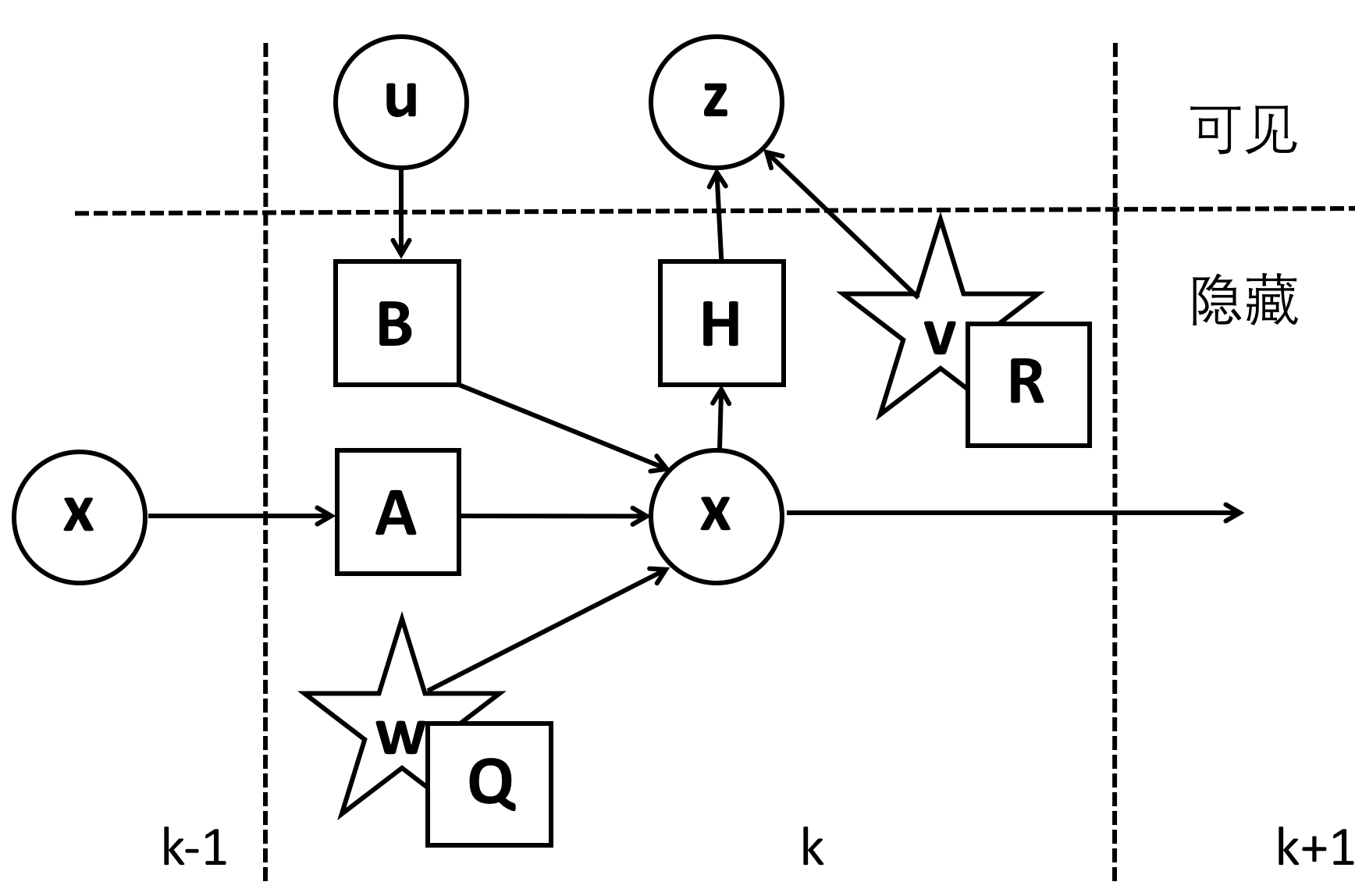图 1. 卡尔曼滤波器模型的描述，其中圆圈代表矢量，方块代表矩阵，星号代表高斯噪声，它的协方差矩阵在其右下角已经标出。
迭代算法
卡尔曼滤波器是一种递归的估计，它需要知道之前一段的历史状态，即$\mathbf{x}_{k-1}$。同时我们又知道当前的一些信息，即控制单元$\mathbf{u}_k$和观测$\mathbf{z}_k$。我们可以粗略地想象这样的迭代算法可以是由两部分组成的，一部分是首先根据前一段的信息去估计当前的状态，第二部分是根据已知的当前信息纠正先前的估计。这听起来像是predictor corrector算法（我不喜欢中文把他翻译成预测校正算法）我更愿意称它为预测子-校正子算法。这样的叫法提醒我们，需要计算一个预测子，之后再计算一个校正子，校正子也就是我们$k$时刻最后的输出。
我们定义$\mathbf{\hat{x}’}_{k}$为$k$时刻先验估计，也就是我们的预测子，
\[\mathbf{\hat{x}'}_k = \mathbf{A} \mathbf{\hat{x}}_{k-1} + \mathbf{B} \mathbf{u}_k, \tag{3}\]其中$\mathbf{\hat{x}}_{k-1}$是k-1时刻的后验估计，也就是我们的校正子，k时候的校正子即为$\mathbf{\hat{x}}_{k}$。有了预测子和校正子，我们可以定义他们和真实的状态$\mathbf{x}_k$之间的误差，对于预测子我们叫先验误差$\mathbf{e}’_k$，对于校正子我们叫后验误差$\mathbf{e}_k$,
\[\mathbf{e}'_k \equiv \mathbf{x}_k - \mathbf{\hat{x}'}_k, \\ \mathbf{e}_k \equiv \mathbf{x}_k - \mathbf{\hat{x}}_k。 \tag{4}\]先验误差的协方差矩阵$\mathbf{P’}_k$和后验误差的协方差矩阵$\mathbf{P}_k$分别为
\[\mathbf{P'}_k = E[\mathbf{e}'_k {\mathbf{e}'_k}^{T}], \\ \mathbf{P}_k = E[\mathbf{e}_k {\mathbf{e}_k}^{T}]。 \tag{5}\]有了这些定义，我们的目标就很明确了，一个好的校正子意味着它与真实的状态之间的误差相差无几。那么，很显然我们希望后验误差尽可能的小，在数学上也就是我们希望协方差矩阵$\mathbf{P}_k$的迹尽可能的小。
我这里不会去推导整个流程，具体怎么得到最小化的流程可以参考Tony Lacey的笔记。根据公式(3)， 有了之前的后验估计$\mathbf{\hat{x}}_{k-1}$， 我可以求出先验估计$\mathbf{\hat{x}’}_k$。但怎么从先验估计计算$k$时刻的后验估计，我们却不清楚。我们大胆假设k时刻的后验估计$\mathbf{\hat{x}}_{k}$和先验估计$\mathbf{\hat{x}’}_{k}$存在如下的关系，
\[\mathbf{\hat{x}}_{k} = \mathbf{\hat{x}’}_{k} + \mathbf{K}_k (\mathbf{z}_k - \mathbf{H} \mathbf{\hat{x}’}_{k})， \tag{6}\]其中我们把$\mathbf{z}_k - \mathbf{H} \mathbf{\hat{x}’}_{k}$称为测量余量，$\mathbf{K}_k$称为卡尔曼增益。毫无疑问整个推导流程必然是找到一个最优的卡尔曼增益，这里我直接给出最优卡尔曼增益的结果，
\[\mathbf{K}_k = \mathbf{P'}_k \mathbf{H}^T (\mathbf{H} \mathbf{P'}_k \mathbf{H}^T + \mathbf{R})^{-1} \tag{7}\]到这里，我们基本上已经得到了整个算法的流程（我们还缺少协方差矩阵的递归公式，这里就不详细介绍了）。下面我就直接给出卡尔曼滤波器的伪代码，
预测：
\[\mathbf{\hat{x}'}_k = \mathbf{A} \mathbf{\hat{x}}_{k-1} + \mathbf{B} \mathbf{u}_k \\ \mathbf{P}'_k = \mathbf{A} \mathbf{P}_{k-1} \mathbf{A}^T + \mathbf{Q}。\]校正：
\[\mathbf{K}_k = \mathbf{P'}_k \mathbf{H}^T (\mathbf{H} \mathbf{P'}_k \mathbf{H}^T + \mathbf{R})^{-1}, \\ \mathbf{\hat{x}}_{k} = \mathbf{\hat{x}’}_{k} + \mathbf{K}_k (\mathbf{z}_k - \mathbf{H} \mathbf{\hat{x}’}_{k}), \\ \mathbf{P}_k = (\mathbf{I} - \mathbf{K}_k \mathbf{H}) \mathbf{P}'_k。\]初始化的时候我们需要假设一个$\mathbf{\hat{x}}_0$和$\mathbf{P}_{0}$。通过不停地递归，我们就可以得到每一步的校正子和后验误差的协方差矩阵了。
程序介绍
程序是建立在一个二维的画布上，我们需要去追踪鼠标的位置。
白色的渐变点代表着对鼠标位置的测量也就是前文所说的$\mathbf{z}_k$，当然速度我们是没法显示的。绿色的线段是卡尔曼滤波器的输出，也就是我们的校正子$\mathbf{\hat{x}_k}$。而蓝色的线段是真实的鼠标位置。
这里先解释一下我是怎么生成白色的渐变点(观测 $\mathbf{z}_k$)。我们可以从GUI的接口知道鼠标的具体位置和这一帧的速度，也就是真实状态$\mathbf{x}_k$。我对这个真实的状态做了一些微扰（高斯噪声），这个高斯噪声被矩阵$\mathbf{N}$来表示，读者如果可以运行这个程序，可以调节协方差矩阵$\mathbf{N}$来控制这些白色渐变点的分布。
二维空间坐标的真实状态$\mathbf{x}_k$可以写作为，
\[\mathbf{x}_k = \begin{bmatrix} x_k \\ y_k \\ \dot{x}_k \\ \dot{y}_k \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & \delta t & 0 \\ 0 & 1 & 0 & \delta t \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} x_{k-1} \\ y_{k-1} \\ \dot{x}_{k-1} \\ \dot{y}_{k-1} \\ \end{bmatrix} + \begin{bmatrix} \delta t^2/2 & 0 \\ 0 & \delta t^2/2 \\ \delta t & 0 \\ 0 & \delta t \end{bmatrix} \times \begin{bmatrix} \ddot{x}_{k-1} \\ \ddot{y}_{k-1} \end{bmatrix}= \mathbf{A} \mathbf{x}_{k-1} + \mathbf{B} \mathbf{u}_k \tag{8}\]其中$\delta t$ 是一个小量，在程序中我设置为一帧的时间，也就是我们每次都是按一帧来更新状态的。在这个简单的系统中，我们没有控制单元$\mathbf{u}_k$，因为我们不知道模型的加速度等（大大地简化了我们的模型）。模型噪声的来源可以假设是一个多维的高斯分布。如果按照中文维基百科的解释，我们也可以认为噪声的来源是来自模型的加速度，这里就不展开了。我们粗暴地认为，
\[\mathbf{x}_k = \mathbf{A} \mathbf{x}_{k-1} + \mathbf{w}_k \tag{9}，\]而$\mathbf{w}_k$满足四维的高斯分布，它的均值为0，其协方差矩阵$\mathbf{Q}$可以通过界面来调节。对于这个简单的系统，我们的观测十分明了，
\[\mathbf{z}_k = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} x_k \\ y_k \\ \dot{x}_k \\ \dot{y}_k \\ \end{bmatrix} + \mathbf{v}_k = \mathbf{H} \mathbf{x}_{k} + \mathbf{v}_k \tag{8}\]噪声$\mathbf{v}_k$的协方差矩阵$\mathbf{R}$也可以通过界面来调节。
这里介绍一下模型参数$\mathbf{Q}$和$\mathbf{R}$，两者是竞争性的关系。读者可以去登录Richard Teammco的网站来模拟滤波器的特性。如果参数$\mathbf{Q}$相对于参数$\mathbf{R}$很小，那么我们认为系统的模型非常准确。如果参数$\mathbf{R}$相对于参数$\mathbf{Q}$很小，那么滤波器认为我们的观测是非常准确的，输出则会接近于观测到的状态。具体请看下面几幅图的示例。
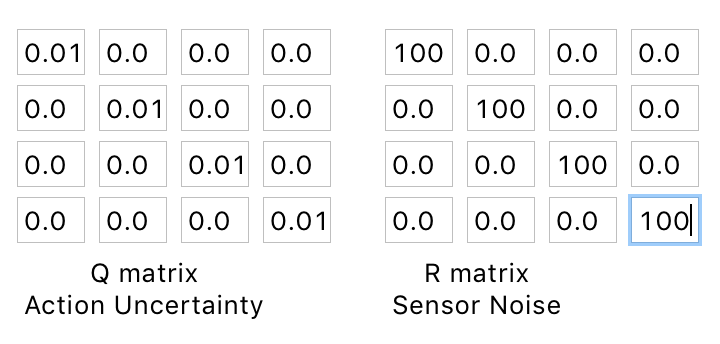||Q|| 远小于 ||R||
滤波器认为模型很准确的情况。
||Q|| 远大于 ||R||
滤波器认为观测很准确的情况。这里几乎拟合了所有观测点。
到这里，我对整个卡尔曼滤波器和鼠标追踪的示例程序就介绍完了，对python感兴趣的同学可以参看我的python代码。