Recently, I was assigned a task to accelerate a program by using a GPU accelerator. After analyzing the original Python program, namely the rigorous coupled wave analysis (RCWA) method, I found that the major time-consuming parts are matrix multiplication, inversion of the matrix, and eigenvalues of non-symmetric matrices. Before we undertake any major code migration tasks, it is important to test the functionality and performance of the matrix operator on different hardware and software platforms to assess the desired acceleration.

Theoretical Performance for various GPU cards

Nvidia provides some specs for consumers. Before we benchmark the some matrix operators, it is essential to have a general understanding of the performance of GPU cards. Below is the theoretical performance for various GPU cards which I might have access to. I obtained these numbers from tech power up. As we can see that, consumer cards like RTX 3060 perform very well at FP32 single precision, which can be understood considering the card’s primary application in the gaming industry. However, to achieve better performance in FP64 double precision, professional cards like Tesla V100 are necessary. For example, A100 has at least 20 times faster speed compared to RTX 4070. The theoretical FLOPS of various cards will be used to understand the benchmark tests below.

	FP32 single [TFLOPS]	FP64 double [TFLOPS]
RTX 3060 12GB	12.74	0.199
RTX 4070 12GB	29.15	0.455
RTX A5000 24GB	27.77	0.434
Tesla V100 DGX 32GB	15.67	7.834
A100 SXM4 80GB	19.49	9.746

Performance of matrix operators of numerical library on platforms

For the hardware platform, I will use Intel Xeon Gold 5220R CPU with a frequency of 2.2GHz, along with Nvidia RTX 3060, Nvidia RTX 4070, and Nvidia RTX A5000. In the future, I might have access to Nvidia Tesla V100 or potentially even more advanced, such as A100. But currently, these hardware platforms are sufficient for me to gather some useful informations. Tests are run on a Linux-based system. The software libraries to be tested include Numpy, CuPy, Pytorch, scikit-cuda, and JAX. All tests are repeated 10 times to measure the average running time. No warm-up procedures were prepared. Below are partial results presented in the figures.

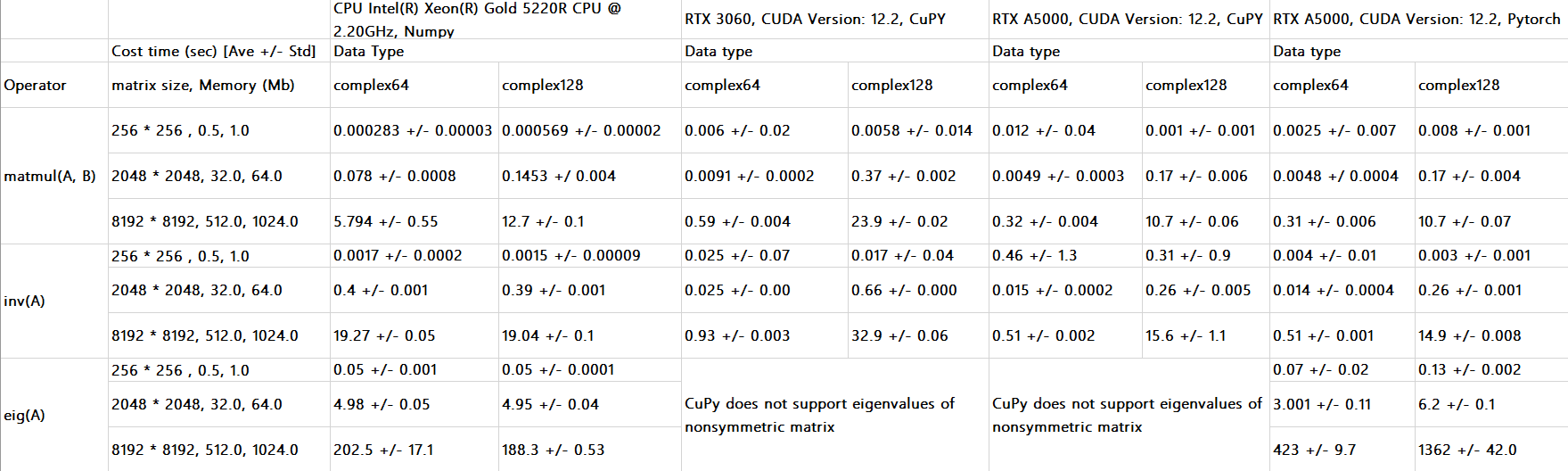Fig. Benchmark of matrix operator on various platforms.

Some conclusions are drawn from the tests:

1. Currently there are no good methods on GPU to compute the eigenvalues of nonsymmetric matrix problems. As we can see in the above figure, Eig(A) of Pytorch consumes more time than it numpy counterpart dealing with the large matrices (8192 * 8192). CuPy does not implement the eig function. JAX only implements the eig function on the CPU backend. The reason behind that is that CUDA and even ScaLapack does not have the alogorithm.
2. For consumer-level cards, such as RTX series tested, they do not perform comparable with CPU on double precision operations. I expect they will perform well on professional GPU cards given the high theoretical FLOPS.
3. We can observe obvious speedup in medium (2048 * 2048) and large (8192 * 8192) matrix operators of single precision on GPU. This is validated by the outstanding number of theoretical performance of GPUs.
4. For small matrix (256 * 256), no obvious speedup is observed in any of the GPU tests.
5. No significant difference was observed in Pytorch and Cupy on the same type of GPU cards. Actually, JAX performs similarly to Pytorch and CuPy. If you simply want to migrate from numpy on CPU to GPU, CuPy is recommended, as its API has the same syntax as numpy’s.

More information about the matrix operators’ performance in CuPy can be found in this reference¹.