数值计算界的鸿篇巨著Numerical Recipes的第三版（简称NR）有一章专门介绍机器学习的分类算法。笔者最近尝试机器学习，便以此书为入门，记下自己的学习过程。高斯混合模型(Gaussian mixture model)是在机器学习里的一个经典算法。它适用于无监督学习(unsupervised learning)下的聚类问题。本篇主要借鉴（照搬）NR的叙述，从原理出发介绍高斯混合模型和 EM (expectation-maximizaton)算法，最后使用python实现其过程, 代码请自取。我个人认为此篇继承了原著NR的如下优点：
- 详细地从原理出发介绍高斯混合模型，而不仅仅陈列出算法的步骤和数学公式。
- 尽可能地少用外部的库函数。
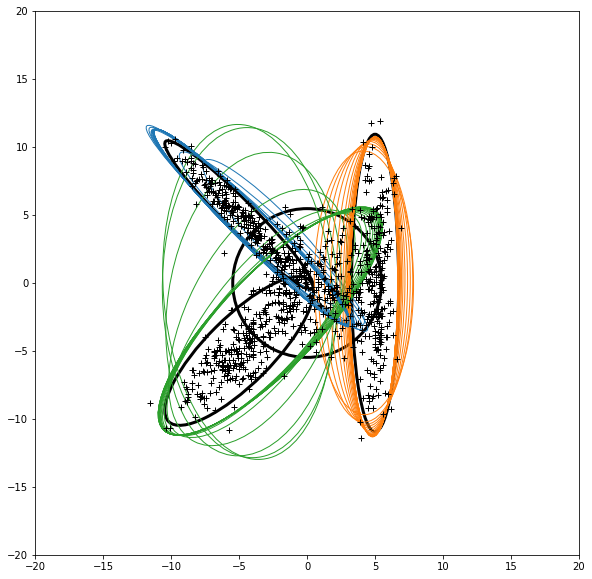图1. NR中聚类的图，展示了EM算法迭代的过程。
模型概述
言归正传，我们现在要解决一个归类的问题：我们有一组数据$N \times M$, $N$是数据的个数，$M$是数据的维度（由于模型的局限，维度最好是个位数）。然后我们希望把这组数据归为$K$个类，每个类用一个多元高斯分布（multivariate gaussian distribution）来表示，比如说单个数据点是2维，那么数据集可以用$K$个2元高斯分布来表征。而事先，我们是不知道这$K$个多元高斯分布的中心位置（means）和协方差矩阵（covariance matrix）的，我们甚至不知道$K$是多少。（当然这些数据是否符合$K$个多元高斯分布的叠加也是未知的。）
那为什么说这是无监督学习呢？因为我们事先也不知道哪些数据点是归于哪个高斯分布的。而这，倒是我们期待从模型和EM算法中得到的结果。对于高斯混合模型来说我们希望知道到底我这个数据点通过算法是归到了哪个类，概率是多少？我们把这个概率记作$p(k|n)$或者$p_{nk}$，其中$0 \le k < K$且$0 \le n < N$。在文献中，$p_{nk}$有时也被称为责任矩阵， 就是说第$K$个类需要对第$n$个数据点负多少点责任。
总结下来，在给定一组数据，比如说$( N \times M )$的矩阵，我们希望估计以下的一组参数:
\[\begin{align} \boldsymbol{\mu}_k \\ \boldsymbol{\Sigma}_k \\ P(k|n) \equiv p_{nk} \\ \end{align} \tag{1}\]其中$\boldsymbol{\mu}_k (K \times M)$是多元高斯分布的中心, $\boldsymbol{\Sigma}_k (K \times M \times M)$是多元高斯分布的协方差矩阵。
我们也会得到一些副产品，比如说$P(k)$, 它表示在第$k$类的数据的个数在总数据个数的占比，等同于任意数据点在第$k$类的概率，很显然$\sum_{k} P(k) = 1$; 我们也可以得到$P(\mathbf{x})$，它表示在任意位置$\mathbf{x}$找到数据点的概率密度； 最重要的是我们可以得到整个数据集的似然函数$\mathscr L (likelihood)$。
其实整个模型的核心就是就是最大化似然函数$\mathscr L$，似然函数正比于，给定拟合参数(比如说这里的$\boldsymbol{\mu}_k$, $\boldsymbol{\Sigma}_k$), 数据集在这套模型下的概率。现在让我们从似然函数出发推导出高斯混合模型的流程。我们假设所有的数据都是独立的，那么似然函数就是在位置$\mathbf{x}_n$找到数据点概率的乘积,
\[\mathscr{L} = \prod\limits_{n} P(\mathbf{x}_n) \tag{2}\]我们可以把$P(\mathbf{x}_n)$拆成来自于$K$个高斯分布的贡献，记作
\[P(\mathbf{x}_n) = \sum\limits_{k}N(\mathbf{x}_n|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)P(k) \tag{3}\]其中$N(\mathbf{x}|\boldsymbol{\mu}, \boldsymbol{\Sigma})$是多元高斯分布，
\[N(\mathbf{x}|\boldsymbol{\mu}, \boldsymbol{\Sigma}) = \frac{1}{(2\pi)^{M/2}\text{det}(\boldsymbol{\Sigma})^{1/2}}\exp(-\frac{1}{2} (\mathbf{x} - \boldsymbol{\mu})^{\text{T}} \cdot \boldsymbol{\Sigma}^{-1} \cdot (\mathbf{x} - \boldsymbol{\mu})) \\ \tag{4}\]从式(2)到式(5)是我们用来计算似然函数 $\mathscr L$的流程，前提当然是我们已经知道了数据和给定的参数比如$\boldsymbol{\mu}_k$, $\boldsymbol{\Sigma}_k$和$P(k)$。在EM算法里面，我么把这个流程叫做期望步骤(Expectation step)或(E-step)。
那我们怎么得到$\boldsymbol{\mu}_k$, $\boldsymbol{\Sigma}_k$ 和$P(k)$呢？
假设我们知道$p_{nk}$。 一个关于一维高斯分布的相关定理告诉我们，这个分布的最大似然平均期望就是所有点的算术平均。那么根据直觉来看，我们可以把它推广到多元高斯分布。因为我们知道了各个点归到给个类的责任矩阵$p_{nk}$， 我们可以求出多元高斯分布的期望平均和期望协方差矩阵。
\[\begin{align} \hat{\boldsymbol{\mu}}_k &= \sum\limits_{n} p_{nk} \mathbf{x}_n / \sum\limits_{n} p_{nk} \\ \hat{\boldsymbol{\Sigma}}_k &= \sum\limits_{n} p_{nk} (\mathbf{x}_n - \hat{\boldsymbol{\mu}}_k) \cdot (\mathbf{x}_n - \hat{\boldsymbol{\mu}}_k)^{\text{T}} / \sum\limits_{n} p_{nk} \\ \end{align} \\ \tag{6}\]类似地，
\[\hat{P}(k) = \frac{1}{N} \sum\limits_{n} p_{nk} \\ \tag{7}\]”$\hat{}$”表示期望，式(6)和(7)是最大化步骤(Maximization step)或(M-step)。
有了E步骤和M步骤，我们只要不停地迭代就能最大化似然函数$\mathscr L$，至少这样的迭代能收敛到一个局部最大值。想要严格地证明EM算法能够最大化似然函数已经超越了本篇的范畴，直觉上告诉我们这样应该是可行的。以下我们归纳以下EM算法的过程：
- 初始化 $\boldsymbol{\mu}_k$, $\boldsymbol{\Sigma}_k$和$P(k)$
- 迭代：先用E步骤得到新的$p_{nk}$和新的$\mathscr{L}$，接着用M步骤得到新的$\boldsymbol{\mu}_k$, $\boldsymbol{\Sigma}_k$和$P(k)$
- 等到$\mathscr{L}$收敛， 退出程序。
下溢和Cholesky分解
下溢
在实际操作中，由于高斯密度往往很小趋近于零，所以会产生下溢（underflow）的问题。为了解决这样的问题，我们往往会选择计算这些密度的对数，而不是他们本身，例如，
\[\ln N(\mathbf{x}|\boldsymbol{\mu}, \boldsymbol{\Sigma}) = -\frac{1}{2} (\mathbf{x} - \boldsymbol{\mu})^{\text{T}} \cdot \boldsymbol{\Sigma}^{-1} \cdot (\mathbf{x} - \boldsymbol{\mu}) - \frac{M}{2}\ln(2\pi) - \frac{1}{2}\ln(\text{det}(\boldsymbol{\Sigma})) \\ \tag{8}\]$-\frac{M}{2}\ln(2\pi)$是常数，在实际操作中（归一化$p_{nk}$）中我们可以忽略这个常数。
在计算式(3)的时候，我们同样也会遇到下溢的问题，因为它们是指数的求和，而每个指数都有可能非常小造成下溢。这里我们可以用到一个叫log-sum-exp公式的技巧。详细参考：Stack Overflow。
\[\ln\Big( \sum\limits_{i} \exp(z_i) \Big) = z_{max} + \ln \Big( \sum\limits_{i} \exp(z_i - z_{max}) \Big) \\ \tag{9}\]很容易证明这个式子是成立的，其中$z_i$是那些小量的对数而$z_{max}$是它们中的最大值。式(9)至少保证了一个指数不会下溢。
这里顺带谈一下在E步骤中计算新的$p_{nk}$的问题。根据式(3-5)，我们可以推出,
\[\ln p_{nk} = -\frac{1}{2} \Big[ (\mathbf{x} - \boldsymbol{\mu})^{\text{T}} \cdot \boldsymbol{\Sigma}^{-1} \cdot (\mathbf{x} - \boldsymbol{\mu}) + \ln(\text{det}\boldsymbol{\Sigma}) \Big] + \ln P(k) \\ \tag{10}\]我们忽略了$-\frac{M}{2}\ln(2\pi)$这个常数因为之后反正需要重新归一化$p_{nk}$， 而它会被抵消掉。根据式(5)，我们可以得到新的$p’_{nk}$ （’代表归一化后的）为
\[p’_{nk} = \frac{p_{nk}}{\sum\limits_{k} p_{nk}} = \exp \Big( \ln p_{nk} - \ln(\sum\limits_{n} p_{nk}) \Big) \tag{11}\]显然上式的计算需要用到log-sum-exp的技巧。
Cholesky分解
我们需要利用Cholesky分解来更有效地计算多元高斯分布，例如，我们需要更高效地计算像$\mathbf{y} \cdot \boldsymbol{\Sigma}^{-1} \cdot \mathbf{y}$这样的表达式。 因为协方差矩阵$\boldsymbol{\Sigma}$是对称且正定的，而Cholesky分解比其他方法需要的操作更少一些，我们有
\[\boldsymbol{\Sigma} = \mathbf{L \cdot L}^{\text{T}} \\ \tag{12}\]其中$\mathbf{L}$是下三角矩阵，有
\[Q = \mathbf{y} \cdot \boldsymbol{\Sigma}^{-1} \cdot \mathbf{y} = |\mathbf{L}^{-1} \cdot \mathbf{y} |^{2} \\ \tag{13}\]其中$\mathbf{L}$是下三角矩阵，有
\[Q = \mathbf{y} \cdot \boldsymbol{\Sigma}^{-1} \cdot \mathbf{y} = |\mathbf{L}^{-1} \cdot \mathbf{y} |^{2} \\ \tag{14}\]由于$\mathbf{L}$是下三角矩阵，那么$\mathbf{L}^{-1} \cdot \mathbf{y}$可以用向后替换(backsubstitution)更为高效地计算。
至此，高斯混合模型已经讲解完毕，在实际运用的过程中，程序可能会出错或者收敛到一个结果很差的局部最小解。程序出错可能有诸多原因，其中一个可能是给定的初始值$\boldsymbol{\mu}_k$不是接近数据点。其余问题我这里不再赘述。
K均值
高斯混合模型的一个简化模型是K均值归类(K-means clustering)。K均值分类不关心概率问题（记住，我们在高斯混合模型中一个重要参数是 $p_{nk}$， 比如说，一个数据点被归为第1类的概率可以是$p_{n1} = 50\%$ ，被归为第2类的概率是$p_{n2}= 50\% $，其余为0）。它只关心我这个数据点被分配到哪个类，也就是说一个数据点只能归属$K$个类中的某个。这里简述一下K均值中EM算法的流程，
- E步骤：根据欧式距离$||\mathbf{x}_n - \boldsymbol{\mu}_k ||$，分配数据点$\mathbf{x}_n$到最近的k类。
- M步骤：重新通过平均k类中的所有数据点 $\mathbf{x}_n$来计算k类的中心$\boldsymbol{\mu}_k $，
收敛的标准是当每个类分配到的数据点不变时，程序可以退出，当然$\boldsymbol{\mu}_k$也不会变动了。$K $均值的收敛可以说是保证的，也就是说不会陷入死循环。尽管K均值看起来很简单，但它还是很有用的：速度快，收敛快。它可以把很多数据点归到一些中心，而这些中心可以作为更高级一些的算法的输入值。